Tag: splines

Splines!

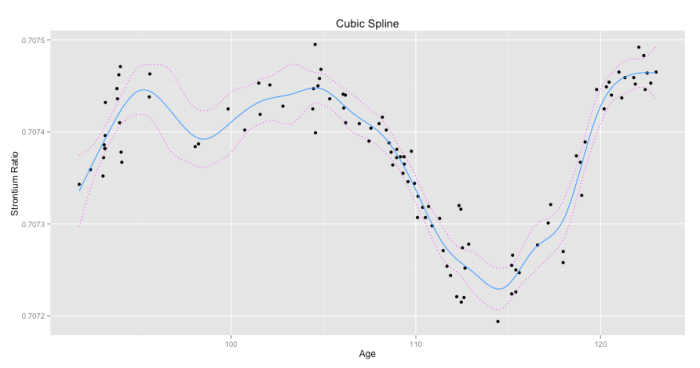
Splines are a popular way to fit data that allow for a good fit when the data has some sort of global curvature (see the graph below for an example). A cubic spline is a popular example. It allows for a cubic polynomial to be fit within some neighborhood between so-called “knots.” So for the graph below you might have a knot at age 0 and another knot at age 50, yet another knot at age 100, and so on. Within each segment of the data defined by these knots you fit a cubic polynomial. You then require that at the knot locations where the different polynomials meet they must join together in a smooth way (this is done by enforcing the first and second derivatives be equal at the knot).

Below a spline with 20 evenly spaced knot locations is shown for some dummy data. I’ve also graphed a 95% confidence interval of the spline predictions in dotted red.

cubic spline

Here’s the code I used to produce it.

# Load libraries
library(reshape)
library(mgcv)
library(ggplot2)
library(data.table)
 
# Load data
setwd("Masked")
data <- read.csv(file = "Masked", header = TRUE)
attach(data)
 
# Create 20 evenly spaced knots
splitDistance <- (max(age) - min(age))/19
knots <- seq(min(age), max(age), by = splitDistance)
 
# Fit a penalized cubic regression spline with 20 evenly spaced 
# knots using cross validation
model <- gam(strontium.ratio ~ s(age, k=20, fx=F, bs="cr", m=2), 
data=data, family=gaussian, sp = .45, knots = list(age = knots))
# Predict points to plot data 
plotPoints <- seq(min(age), max(age), by = .05)
yHat <- predict.gam(model, list(age = plotPoints), se.fit = TRUE)
 
# Create 95% confidence interval
upper95 <- yHat[[1]] + 1.96*yHat[[2]]
lower95 <- yHat[[1]] - 1.96*yHat[[2]]
 
# Prepare data for plotting
spline <- as.data.frame(cbind(plotPoints,yHat[[1]]))
setnames(spline,"V2","value")
CI <- as.data.frame(cbind(plotPoints,upper95,lower95))
CI <- melt(CI, id = "plotPoints", 
variable_name = "Confidence.Interval")
 
# Plot data
ggplot() +
geom_point(data = data, aes(x = age, y = strontium.ratio)) +
geom_line(data=spline, aes(x = plotPoints, y = value), 
colour = '#3399ff') +
geom_line(data=CI, aes(x = plotPoints, y = value, 
group = Confidence.Interval),linetype="dotted",colour = '#ff00ff') +
ggtitle("Cubic Spline") + 
xlab("Age") + 
ylab("Strontium Ratio")

Created by Pretty R at inside-R.org

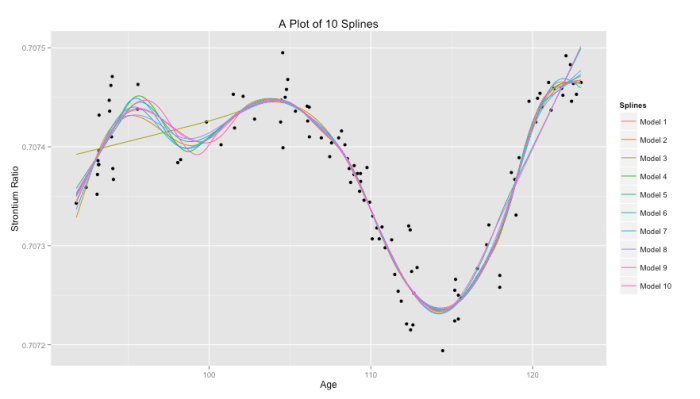
To show the effect of knot placement we can generate 20 random knot locations for multiple models and compare them. Since these are so-called natural splines linearity is enforced after the last knot. Here, Model 3 had it’s first knot generated quite far on the righthand side of the Age axis and so it’s linear to the left of that point.

10 Splines

Again, here’s the code.

# Create 10 models with random knot placement
set.seed(35)
models <- as.data.frame(lapply(1:10,
                        FUN = function(i) {
                        knots <- sort(runif(20, min(age), 
                        max(age)))
                        model <- gam(strontium.ratio ~ 
                        s(age, k=20, fx=F, bs="cr", m=2), 
                        data=data, family=gaussian, 
                        method="GCV.Cp", 
                        knots = list(age = knots))
                        return(predict(model,
                        list(age = plotPoints)))
                        }))
 
colnames(models) <- lapply(1:10,
                    FUN = function(i) {
                    return(paste("Model",i))
                    })
 
# Plot splines
models <- cbind(plotPoints, models)
models <- melt(models, id = "plotPoints", variable_name = "Splines")
 
ggplot() +
geom_point(data = data, aes(x = age, y = strontium.ratio)) +
geom_line(data = models, aes(x = plotPoints, y = value, 
group = Splines, colour = Splines)) +
ggtitle("A Plot of 10 Splines") + 
xlab("Age") + 
ylab("Strontium Ratio")

Created by Pretty R at inside-R.org