Tag: distribution

Distribution Convergence

Let’s do a problem from Chapter 5 of All of Statistics.

Suppose X_1, \dots X_n \sim \text{Uniform(0,1)} . Let Y_n = \bar{X_n}^2 . Find the limiting distribution of Y_n .

Note that we have Y_n = \bar{X_n}\bar{X_n}

Recall from Theorem 5.5(e) that if X_n \rightsquigarrow X and Y_n \rightsquigarrow c  then X_n Y_n \rightsquigarrow cX .

So the question becomes does X_n \rightsquigarrow c  so that we can use this theorem? The answer is yes. Recall that from Theorem 5.4(b) X_n \overset{P}{\longrightarrow} X implies that X_n \rightsquigarrow X . So if we can show that we converge to a constant in probability we know that we converge to the constant in distribution. Let’s show that \bar{X}_n \overset{P}{\longrightarrow} c . That’s easy. The law of large numbers tells us that the sample average converges in probability to the expectation. In other words \bar{X}_n \overset{P}{\longrightarrow} \mathbb{E}[X] . Since we are told that X_i is i.i.d from a Uniform(0,1) we know the expectation is \mathbb{E}[X] = .5 .

Putting it all together we have that:

Y_n = \bar{X_n}^2
Y_n = \bar{X_n}\bar{X_n}
Y_n \rightsquigarrow \mathbb{E}[X]\mathbb{E}[X] (through the argument above)
Y_n \rightsquigarrow (.5)(.5)
Y_n \rightsquigarrow .25

We can also show this by simulation in R, which produces this chart:

y_convergence

Indeed we also get the answer 0.25. Here is the R code used to produce the chart above:

# Load plotting libraries
library(ggplot2)
library(ggthemes)

# Create Y = g(x_n)
g = function(n) {
  return(mean(runif(n))^2)
}

# Define variables
n = 1:10000
Y = sapply(n, g)

# Plot
set.seed(10)
df = data.frame(n,Y)
ggplot(df, aes(n,Y)) +
  geom_line(color='#3498DB') +
  theme_fivethirtyeight() +
  ggtitle('Distribution Convergence of Y as n Increases')

Distribution Mean Convergence

Suppose we want to simulate 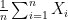\frac{1}{n}\sum_{i=1}^{n} X_i for X_1, X_2, \dots , X_n \sim N(0, 1) , n = 1, \dots , 10,000 . Suppose we want to do the same for the Cauchy distribution.

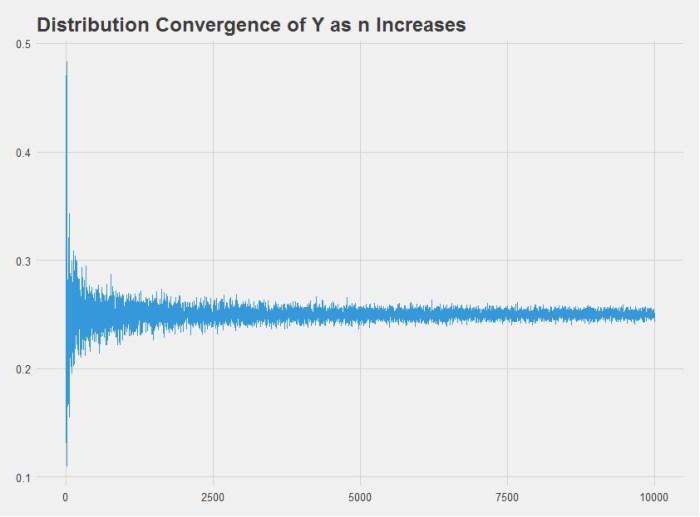
In other words, we want to draw several random variables from a normal distribution and then take the average. As 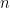n increases we should get closer to the mean of the distribution we’re drawing from, 0 in this case.

The R code below will do this. It produces this graph:
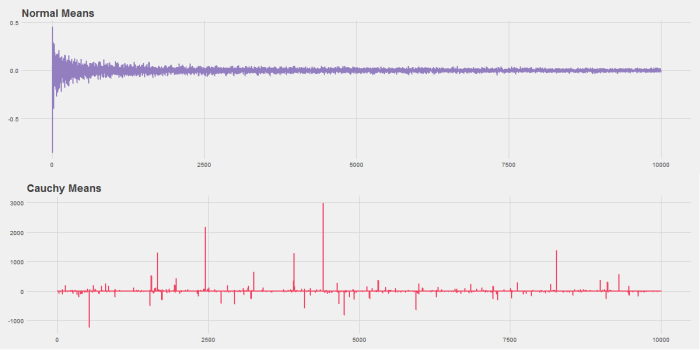
ch3-pr9

Notice that while the Normal distribution converges quickly the Cauchy never does. This is because the Cauchy distribution has fat tails and so extreme observations are common.

################################################################
# R Simulation
# James McCammon
# 2/20/2017
################################################################
# This script goes through the simulation of plotting both normal
# and Cauchy means for random vectors of size 1 to 10,000. It
# also demonstrates function creation and plotting.
# Highlight desired section and click "Run."

# Set working directory as needed
setwd("~/R Projects/All of Statistics")

###
# Calculate means and plot using base R
###

    # Set seed for reproducibility
    set.seed(271)
    
    #
    # Version 1: Simple
    #
    n = seq(from=1, to=10000, by=1)
    y=sapply(n, FUN=function(x) sum(rnorm(x))/x)
    plot(n, y, type="l")
    
    #
    # Version 2: Define a function
    #
    sim = function(x, FUN) {
      sapply(x, FUN=function(x) sum(FUN(x))/x)  
    }
    
    # Use function to plot normal means
    x = seq(from=1, to=10000, by=1)
    y1 = sim(x, rnorm)
    plot(x, y1, type="l")
    
    # Use function to plot Cauchy means
    y2 = sim(x, rcauchy)
    plot(x, y2, type="l")
    
    #
    # Version 3: More complex function
    #
    
    # This function has:
    # (1) error checking
    # (2) extra argument options
    # (3) the ability to input any distribution R supports
    sim = function(x, FUN, ...) {
      if(!is.character(FUN)) stop('Please enter distribution as string.')
      dists = c('rnorm',
                'rbeta',
                'rbinom',
                'rcauchy',
                'rchisq',
                'rexp',
                'rf',
                'rgamma',
                'rgeom',
                'rhyper',
                'rlnorm',
                'rmultinom',
                'rnbinom',
                'rpois',
                'rt',
                'runif',
                'rweibull')
      if(is.na(match(FUN, dists))) stop(paste('Please enter a valid distribution from one of:', paste(dists, collapse=', ')))
      FUN = get(FUN)
      sapply(x, FUN=function(x) sum(FUN(x, ...))/x)  
    }
    
    # We have to define our function in string form.
    # This will throw error 1.
    test1 = sim(x, rnorm)
    
    # We have to input a distribution R supports.
    # This will throw error 2.
    test2 = sim(x, 'my_cool_function')
    
    # We can input additional arguments like the
    # mean, standard deviations, or other shape parameters.
    test3 = sim(x, 'rnorm', mean=10, sd=2)

####
# Using ggplot2 to make pretty graph
###

    # Load libraries
    library(ggplot2)
    library(ggthemes)
    library(gridExtra)
    
    png(filename='Ch3-Pr9.png', width=1200, height=600)
    
      df1 = cbind.data.frame(x, y1)
      p1 = ggplot(df1, aes(x=x, y=y1)) + 
        geom_line(size = 1, color='#937EBF') + 
        theme_fivethirtyeight() +
        ggtitle("Normal Means")
      
      df2 = cbind.data.frame(x, y2)
      p2 = ggplot(df2, aes(x=x, y=y2)) + 
        geom_line(size = 1, color='#EF4664') + 
        theme_fivethirtyeight() +
        ggtitle("Cauchy Means")
      
      # Save charts
      grid.arrange(p1,p2,nrow=2,ncol=1)
      
    dev.off()
    # Print charts to screen
    grid.arrange(p1,p2,nrow=2,ncol=1)