Kenneth Arrow – The Polymath

The great economist Kenneth Arrow has passed away and the New York Times had a wonderful story about him in their obituary.

Professor Arrow was widely hailed as a polymath, possessing prodigious knowledge of subjects far removed from economics. Eric Maskin, a Harvard economist and fellow Nobel winner, told of a good-natured conspiracy waged by junior faculty to get the better of Professor Arrow, even if artificially. They all agreed to study the breeding habits of gray whales — a suitably abstruse topic — and gathered at an appointed date at a place where Professor Arrow would be sure to visit.

When, as expected, he showed up, they were talking out loud about the theory by a marine biologist — last name, Turner — which purported to explain how gray whales found the same breeding spot year after year. As Professor Maskin recounted the story, “Ken was silent,” and his junior colleagues amused themselves that they had for once bested their formidable professor.

Well, not so fast.

Before leaving, Professor Arrow muttered, “But I thought that Turner’s theory was entirely discredited by Spencer, who showed that the hypothesized homing mechanism couldn’t possibly work.”

A Quick Little Proof

Let’s prove that $\sqrt{3}$ is irrational. An irrational number is one that cannot be written in the form $\frac{a}{b}$ , where $a$ and $b$ are both integers; in other words there is no repeating pattern in it’s decimal.

First, let’s prove that if $n^2$ is a multiple of $3$ then so is $n$ . Assume that $n$ is not a multiple of $3$ . Then $n$ can be written as: $n = 3m + \ell$ where $\ell \in \{1,2\}$ . Then $n^2 = 9m^2 + 6m\ell + \ell^2$ . We can factor out a $3$ , so $n^2 = 3(3m^2 + 2m\ell) + \ell^2$ . This implies $n^2$ is not a multiple of $3$ since it’s an integer times $3$ plus a number that isn’t a multiple of $3$ (that’s the $\ell$ part). We have proved the contrapositive which implies our original proposition ( $P \Rightarrow Q$ is the same as $\neg Q \Rightarrow \neg P$ ).

Now let’s move on to the main proof. Assume, by way of contradiction that the square root of $3$ is rational. If the square root of $3$ is rational then we can write $\sqrt{3} = \frac{a}{b}$ with $a$ and $b$ not sharing any common factors. We can do some math: $3 = \frac{a^2}{b^2}$ which means $3b^2 = a^2$ . But this means $a^2$ is a multiple of $3$ since it’s an integer times $3$ . We just proved that if $n^2$ is a multiple of $3$ then so is $n$ . This means that $a$ is a multiple of 3. But if $a$ is a multiple of $3$ it can be written as $3m$ . Let’s plug this in to get $3b^2 = (3m)^2$ , simplifying we get that $3b^2 = 9m^2$ . Let’s divide through by $3$ to get $b^2 = 3m^2$ . This means that $b^2$ is a multiple of $3$ since it’s $3$ times an integer. But again, if $b^2$ is a multiple of $3$ then so is $b$ . We started off by assuming that $a$ and $b$ had no common factors and we just showed that they share a common factor of $3$ . We’ve derived a contradiction to our proposition that $\sqrt{3}$ is rational, therefore it must be irrational.

Second Life’s Effect on the Disabled

As Fran and Barbara tell it, the more time Fran spent in Second Life, the younger she felt in real life. Watching her avatar hike trails and dance gave her the confidence to try things in the physical world that she hadn’t tried in a half decade — like stepping off a curb or standing up without any help. These were small victories, but they felt significant to Fran.

That is from a fascinating new article on the effect Second Life has had on the disability community. It seems that immersion in online worlds gets a lot of push back these days, but (at least as this article tells it) immersive virtual worlds can be a major positive influence for those across the disability spectrum.

Here is a short video about Fran, the main character in the story.

Stock Price Simulation

Larry Wasserman presents an interesting simulation in Problem 11, Chapter 3 of All of Statistics. The problem asks you to simulate the stock market by modeling a simple random walk. With probability 0.5 the price of the stock goes down $1 and with probability 0.5 the stock prices goes up $1. You may recognize this as the same setup in our two simple random walk examples modeling a particle on the real line.

This simulation is interesting because Wasserman notes that even with an equal probability of the stock moving up and down we’re likely to see patterns in the data. I ran some simulations that modeled the change in stock price over the course of 1,000 days and grabbed a couple of graphs to illustrate this point. For example, look at the graph below. It sure looks like this is a stock that’s tanking! However, it’s generated with the random walk I just described.

stock_plot1

Even stocks that generally hover around the origin seem to have noticeable dips and peaks that look like patterns to the human eye even though they are not.

stock_plot2

If we run the simulation multiple times it’s easy to see that if you consider any single stock it’s not so unlikely to get large variations in price (the light purple lines). However, when you consider the average price of all stocks, there is very little change over time as we would expect (the dark purple line).

stock_plot3

Here is the R code to calculate the random walk and generate the last plot:

################################################################
# R Simulation
# James McCammon
# 2/20/2017
################################################################
# This script goes through the simulation of changes in stock
# price data.

# Load plotting libraries
library(ggplot2)
library(ggthemes)
library(reshape2)

#
# Simulate stock price data with random walk
#
    n = 1000 # Walk n steps
    p = .5 # Probability of moving left
    trials = 100 # Num times to repeate sim
    # Run simulation
    rand_walk = replicate(trials, cumsum(sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))))

#
# Prepare data for plotting
#
    all_walks = melt(rand_walk)
    avg_walk = cbind.data.frame(
      'x' = seq(from=1, to=n, by=1),
      'y' = apply(rand_walk, 1, mean)
    )

#
# Plot data
#
    ggplot() + 
      geom_line(data=all_walks, aes(x=Var1, y=value, group=Var2), color='#BCADDC', alpha=.5) +
      geom_line(data=avg_walk, aes(x=x, y=y), size = 1.3, color='#937EBF') +
      theme_fivethirtyeight() +
      theme(axis.title = element_text()) +
      xlab('Days') +
      ylab('Change in Stock Price (in $)') +
      ggtitle("Simulated Stock Prices")

Simple Random Walk – Method 2

Suppose we consider a simple random walk. A particle starts at initial position $z_i$ and moves one unit to the left with probability $p$ and moves one unit to the right with probability $1-p$ . What is the expected position $\mathbb{E}[X_n]$ of the particle after $n$ steps?

In a previous post I presented a method to solve this by iteration. I’d like to present a different method to solve the problem here.

Recall we have:

$X_i = \bigg\{ \begin{tabular}{cc} p & x = -1 \\ 1-p & x = 1 \end{tabular}$

We give it some thought we can see that after $n$ steps we’ve simply added up our random variables to get our final location. We could define a new random variable:

$Y = \sum_{i=1}^{n} X_i$

So now all we need to do is take the expected value of $Y$ . We can use rules of expected value to bring the expectation inside the summation and take the expectation of each individual $X_i$ as we normally would.

$\mathbb{E}[Y] = \mathbb{E}\big[\sum_{i=1}^{n} X_i \big]$
$\mathbb{E}[Y] = \sum_{i=1}^{n} \mathbb{E}[X_i]$
$\mathbb{E}[Y] = \sum_{i=1}^{n} -1 \cdot p + 1 \cdot (1-p)$
$\mathbb{E}[Y] = \sum_{i=1}^{n} 1 - 2p$
$\mathbb{E}[Y] = n(1 - 2p)$

This is the same answer we got via the iteration method. This also makes our R simulation easier. Recall we has this setup:

################################################################
# R Simulation
################################################################
# Generate random walk
rand_walk = function (n, p, z) {
  walk = sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))
  for (i in 1:n) {
    z = z + walk[i]
  }
  return(z)
}

n = 1000 # Walk n steps
p = .3 # Probability of moving left
z = 0 # Set initial position to 0
trials = 10000 # Num times to repeate sim
# Run simulation
X = replicate(trials, rand_walk(n,p,z))

Our code now becomes:

################################################################
# R Simulation
################################################################
n = 1000 # Walk n steps
p = .3 # Probability of moving left
trials = 10000 # Num times to repeate sim
# Run simulation
X = replicate(trials, sum(sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))))

# Calculate empirical and theoretical results
empirical = mean(X)
theoretical = n*(1-2*p)
percent_diff = abs((empirical-theoretical)/empirical)*100

# print to console
empirical
theoretical
percent_diff

Notice that for our random walk we can replace this function:

rand_walk = function (n, p, z) {
  walk = sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))
  for (i in 1:n) {
    z = z + walk[i]
  }
  return(z)
}
X = replicate(trials, rand_walk(n,p,z))

With the simpler:

X = replicate(trials, sum(sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))))

Additionally, in this second method we don’t need to specify an initial position since we assume from the beginning it’s zero. Of course both methods complete the same task, but they use different conceptual models. The first uses an iteration model, while the latter completes the “iteration” in a single step.

What Jane Jacobs Got Right and Wrong

The sad truth is that the saints we revere for thinking for themselves almost always end up thinking by themselves. We are disappointed to find that the self-taught are also self-centered, although a moment’s reflection should tell us that you have to be self-centered to become self-taught. (The more easily instructed are busy brushing their teeth, as pledged.) The independent-minded philosopher-saints are so sure of themselves that they often lose the discipline of any kind of peer review, formal or amateur. They end up opinionated, and alone.

That is from Adam Gopnik’s New Yorker article “Jane Jacobs’s Street Smarts” about what Jacobs got both right and wrong about cities over the course of her career.

There is, of course, a focus on “The Death and Life,” by far her most famous work.

Two core principles emerge from the book’s delightful and free-flowing observational surface. First, cities are their streets. Streets are not a city’s veins but its neurology, its accumulated intelligence. Second, urban diversity and density reinforce each other in a virtuous circle. The more people there are on the block, the more kinds of shops and social organizations—clubs, broadly put—they demand; and, the more kinds of shops and clubs there are, the more people come to seek them. You can’t have density without producing diversity, and if you have diversity things get dense. The two principles make it plain that any move away from the street—to an encastled arts center or to plaza-and-park housing—is destructive to a city’s health. Jacobs’s idea can be summed up simply: If you don’t build it, they will come.

The book still has relevant today, but not all of it has held up.

Books written in a time of crisis can make bad blueprints for a time of plenty, as polemics made in times of war are not always the best blueprint for policies in times of peace. Jane Jacobs wrote “Death and Life” at a time when it was taken for granted that American cities were riddled with cancer. Endangered then, they are thriving now, with the once abandoned downtowns of Pittsburgh and Philadelphia and even Cleveland blossoming. Our city problems are those of overcharge and hyperabundance—the San Francisco problem, where so many rich young techies have crowded in to enjoy the city’s street ballet that there’s no room left for anyone else to dance.

…

The old neighborhood is helpless in the face of new pressures, because it had depended on older versions of the same pressures, ones that Jacobs was not entirely willing to name or confront. What kept her street intact was not a mysterious equilibrium of types, or magic folk dancing, but market forces. The butcher and the locksmith on Hudson Street were there because they could make a profit on meat and keys. They weren’t there to dance; they were there to earn. The moment that Mr. Halpert and Mr. Goldstein can’t turn that profit—or that Starbucks and Duane Reade can pay the landlord more—the tempo changes.

Distribution Mean Convergence

Suppose we want to simulate 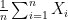$\frac{1}{n}\sum_{i=1}^{n} X_i$ for $X_1, X_2, \dots , X_n \sim N(0, 1)$ , $n = 1, \dots , 10,000$ . Suppose we want to do the same for the Cauchy distribution.

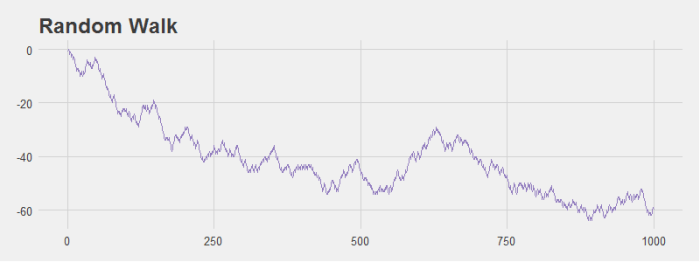
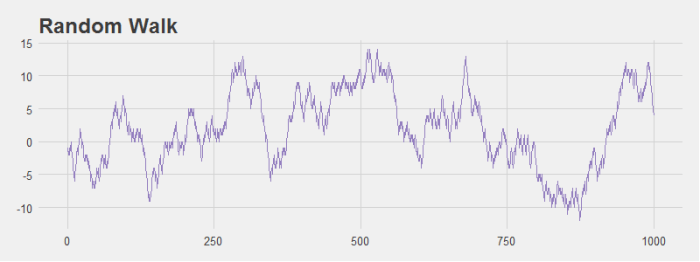
In other words, we want to draw several random variables from a normal distribution and then take the average. As 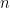$n$ increases we should get closer to the mean of the distribution we’re drawing from, 0 in this case.

The R code below will do this. It produces this graph:
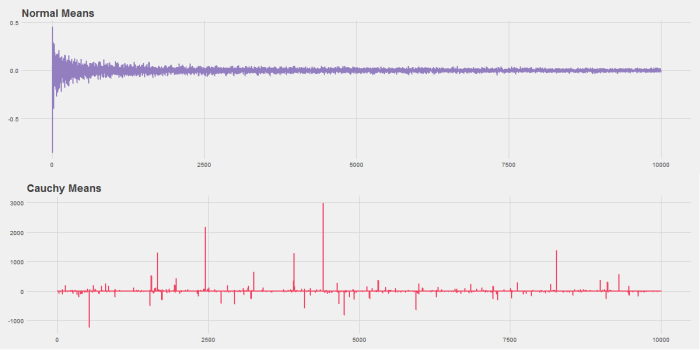
ch3-pr9

Notice that while the Normal distribution converges quickly the Cauchy never does. This is because the Cauchy distribution has fat tails and so extreme observations are common.

################################################################
# R Simulation
# James McCammon
# 2/20/2017
################################################################
# This script goes through the simulation of plotting both normal
# and Cauchy means for random vectors of size 1 to 10,000. It
# also demonstrates function creation and plotting.
# Highlight desired section and click "Run."

# Set working directory as needed
setwd("~/R Projects/All of Statistics")

###
# Calculate means and plot using base R
###

    # Set seed for reproducibility
    set.seed(271)
    
    #
    # Version 1: Simple
    #
    n = seq(from=1, to=10000, by=1)
    y=sapply(n, FUN=function(x) sum(rnorm(x))/x)
    plot(n, y, type="l")
    
    #
    # Version 2: Define a function
    #
    sim = function(x, FUN) {
      sapply(x, FUN=function(x) sum(FUN(x))/x)  
    }
    
    # Use function to plot normal means
    x = seq(from=1, to=10000, by=1)
    y1 = sim(x, rnorm)
    plot(x, y1, type="l")
    
    # Use function to plot Cauchy means
    y2 = sim(x, rcauchy)
    plot(x, y2, type="l")
    
    #
    # Version 3: More complex function
    #
    
    # This function has:
    # (1) error checking
    # (2) extra argument options
    # (3) the ability to input any distribution R supports
    sim = function(x, FUN, ...) {
      if(!is.character(FUN)) stop('Please enter distribution as string.')
      dists = c('rnorm',
                'rbeta',
                'rbinom',
                'rcauchy',
                'rchisq',
                'rexp',
                'rf',
                'rgamma',
                'rgeom',
                'rhyper',
                'rlnorm',
                'rmultinom',
                'rnbinom',
                'rpois',
                'rt',
                'runif',
                'rweibull')
      if(is.na(match(FUN, dists))) stop(paste('Please enter a valid distribution from one of:', paste(dists, collapse=', ')))
      FUN = get(FUN)
      sapply(x, FUN=function(x) sum(FUN(x, ...))/x)  
    }
    
    # We have to define our function in string form.
    # This will throw error 1.
    test1 = sim(x, rnorm)
    
    # We have to input a distribution R supports.
    # This will throw error 2.
    test2 = sim(x, 'my_cool_function')
    
    # We can input additional arguments like the
    # mean, standard deviations, or other shape parameters.
    test3 = sim(x, 'rnorm', mean=10, sd=2)

####
# Using ggplot2 to make pretty graph
###

    # Load libraries
    library(ggplot2)
    library(ggthemes)
    library(gridExtra)
    
    png(filename='Ch3-Pr9.png', width=1200, height=600)
    
      df1 = cbind.data.frame(x, y1)
      p1 = ggplot(df1, aes(x=x, y=y1)) + 
        geom_line(size = 1, color='#937EBF') + 
        theme_fivethirtyeight() +
        ggtitle("Normal Means")
      
      df2 = cbind.data.frame(x, y2)
      p2 = ggplot(df2, aes(x=x, y=y2)) + 
        geom_line(size = 1, color='#EF4664') + 
        theme_fivethirtyeight() +
        ggtitle("Cauchy Means")
      
      # Save charts
      grid.arrange(p1,p2,nrow=2,ncol=1)
      
    dev.off()
    # Print charts to screen
    grid.arrange(p1,p2,nrow=2,ncol=1)

On Rudeness

I give [the saleswoman] the dress, and she goes away. I find that I no longer want to be in the shop. I don’t want to try on the dress. I don’t want to take my clothes off or look at myself in a mirror. I consider quietly leaving while the assistant is gone, but the fact that I have caused the dress to be put in the fitting room is too significant. Perhaps it will be transformative after all.

That paragraph connect with me as I so often experience these little moments of social anxiety myself.

Perhaps surprisingly that paragraph is from a new and wonderful essay in The New York Times Magazine called “The Age of Rudeness” by Rachel Cusk.

I consider the role that good manners might play in the sphere of rat-eating, and it seems to me an important one. As one who has never been tested, who has never endured famine or war or extremism or even discrimination, and who therefore perhaps does not know whether she is true or false, brave or a coward, selfless or self-serving, righteous or misled, it would be good to have something to navigate by.

There are many, many other points of interest.

…I understood rudeness to be essentially a matter of verbal transgression: It could be defined within the morality of language, without needing to prove itself in a concrete act. A concrete act makes language irrelevant. Once words have been superseded by actions, the time for talking has passed. Rudeness, then, needs to serve as a barrier to action. It is what separates thought from deed; it is the moment when wrongdoing can be identified, in time to stop the wrong from having to occur. Does it follow, then, that a bigoted remark — however ugly to hear — is an important public interface between idea and action? Is rudeness a fundamental aspect of civilization’s immunity, a kind of antibody that is mobilized by the contagious presence of evil?

Or how about:

The liberal elite, as far as I am aware, do not make death threats. Is this because they have better manners? Do they in fact wish that their enemies were dead but would just never say so? And if they do wish it — albeit politely, in the manner of a white lie — is the sin somehow less cardinal for being courteous?

Beautiful sentences throughout:

The moral power of individuality and the poetic power of suffering are the two indispensable components of truth.

Highly recommended.

West Virginia State Board of Education v. Barnette

I have always loved reading Supreme Court Decisions. I think the writing is much more beautiful and accessible that most people realize. Here are a few passages from the famous case West Virginia State Board of Education v. Barnette.

The very purpose of a Bill of Rights was to withdraw certain subjects from the vicissitudes of political controversy, to place them beyond the reach of majorities and officials, and to establish them as legal principles to be applied by the courts. One’s right to life, liberty, and property, to free speech, a free press, freedom of worship and assembly, and other fundamental rights may not be submitted to vote; they depend on the outcome of no elections.

…

These principles grew in soil which also produced a philosophy that the individual was the center of society, that his liberty was attainable through mere absence of governmental restraints, and that government should be entrusted with few controls, and only the mildest supervision [p640] over men’s affairs. We must transplant these rights to a soil in which the laissez-faire concept or principle of noninterference has withered, at least as to economic affairs, and social advancements are increasingly sought through closer integration of society and through expanded and strengthened governmental controls. These changed conditions often deprive precedents of reliability, and cast us more than we would choose upon our own judgment. But we act in these matters not by authority of our competence, but by force of our commissions.

…

Struggles to coerce uniformity of sentiment in support of some end thought essential to their time and country have been waged by many good, as well as by evil, men. Nationalism is a relatively recent phenomenon, but, at other times and places, the ends have been racial or territorial security, support of a dynasty or regime, and particular plans for saving souls. As first and moderate methods to attain unity have failed, those bent on its accomplishment must resort to an ever-increasing severity. [p641] As governmental pressure toward unity becomes greater, so strife becomes more bitter as to whose unity it shall be. Probably no deeper division of our people could proceed from any provocation than from finding it necessary to choose what doctrine and whose program public educational officials shall compel youth to unite in embracing. Ultimate futility of such attempts to compel coherence is the lesson of every such effort from the Roman drive to stamp out Christianity as a disturber of its pagan unity, the Inquisition, as a means to religious and dynastic unity, the Siberian exiles as a means to Russian unity, down to the fast failing efforts of our present totalitarian enemies. Those who begin coercive elimination of dissent soon find themselves exterminating dissenters. Compulsory unification of opinion achieves only the unanimity of the graveyard.

It seems trite but necessary to say that the First Amendment to our Constitution was designed to avoid these ends by avoiding these beginnings. There is no mysticism in the American concept of the State or of the nature or origin of its authority. We set up government by consent of the governed, and the Bill of Rights denies those in power any legal opportunity to coerce that consent. Authority here is to be controlled by public opinion, not public opinion by authority.

The case is made difficult not because the principles of its decision are obscure, but because the flag involved is our own. Nevertheless, we apply the limitations of the Constitution with no fear that freedom to be intellectually and spiritually diverse or even contrary will disintegrate the social organization. To believe that patriotism will not flourish if patriotic ceremonies are voluntary and spontaneous, instead of a compulsory routine, is to make an unflattering estimate of the appeal of our institutions to free minds. We can have intellectual individualism [p642] and the rich cultural diversities that we owe to exceptional minds only at the price of occasional eccentricity and abnormal attitudes. When they are so harmless to others or to the State as those we deal with here, the price is not too great. But freedom to differ is not limited to things that do not matter much. That would be a mere shadow of freedom. The test of its substance is the right to differ as to things that touch the heart of the existing order.

If there is any fixed star in our constitutional constellation, it is that no official, high or petty, can prescribe what shall be orthodox in politics, nationalism, religion, or other matters of opinion, or force citizens to confess by word or act their faith therein. If there are any circumstances which permit an exception, they do not now occur to us. [n19]

We think the action of the local authorities in compelling the flag salute and pledge transcends constitutional limitations on their power, and invades the sphere of intellect and spirit which it is the purpose of the First Amendment to our Constitution to reserve from all official control.

The decision of this Court in Minersville School District v. Gobitis, and the holdings of those few per curiam decisions which preceded and foreshadowed it, are overruled, and the judgment enjoining enforcement of the West Virginia Regulation is

Affirmed.

Simple Random Walk – Method 1

I will calculate the expected value using two different methods. The second method is simpler, but I’ll start using an iteration method.

Our PMF is:

$f_X(x) = \bigg\{ \begin{tabular}{cc} p & x = -1 \\ 1-p & x = 1 \end{tabular}$

Let’s set our initial position as:
$n=0: \quad \mathbb{E}[X_0] = z_i$

After one step our expected position is then:
$n=1: \quad \mathbb{E}[X_1] = (z_i - 1)p + (z_i + 1)(1 - p)$
$n=1: \quad \mathbb{E}[X_1] = z_{i}p - p + z_i + 1 - z_{i}p - p$
$n=1: \quad \mathbb{E}[X_1] = z_i + 1 - 2p$

Great, let’s try iterating one more to see what we get. Note that at $n=2$ our position is now the result from $n=1$ , $z_i + 1 - 2p$ .
$n=2: \quad \mathbb{E}[X_2] = (z_i + 1 - 2p - 1)p + (z_i + 1 - 2p + 1)(1 - p)$
$n=2: \quad \mathbb{E}[X_2] = z_{i}p - 2p^2 + Z_i - 2p + 2 - z_{i}p + 2p^2 - 2p$
$n=2: \quad \mathbb{E}[X_2] = z_i + 2(1 - 2p)$

If we keep iterating we will see that $\mathbb{E}[X_n] = z_i + n(1 - 2p)$ . But we can prove this formally through induction. We’ve already done our base case, so let’s now do the induction step. We will assume that $\mathbb{E}[X_n] = z_i + n(1 - 2p)$ is true and show that it is also true for $n + 1$ .

$\mathbb{E}[X_{n+1}] = (z_i + n(1 - 2p) - 1)p + (z_i + n(1 - 2p) + 1)(1 - p)$
$\mathbb{E}[X_{n+1}] = (z_i + n - 2pn - 1)p + (z_i + n - 2pn + 1)(1 - p)$
$\mathbb{E}[X_{n+1}] = z_{i}p + pn - 2p^{2}n - p + z_i + n - 2pn + 1 -z_{i}p - pn + 2p^{2}n - p$
$\mathbb{E}[X_{n+1}] = - p + z_i + n - 2pn + 1 - p$
$\mathbb{E}[X_{n+1}] = z_i + (n + 1)(1 - 2p)$

Thus our induction step holds and we have shown that $\mathbb{E}[X_n] = z_i + n(1 - 2p)$ .

Because we chose our initial starting position $z_i$ to be arbitrary, we might as well set it to 0 to obtain a final result of $\mathbb{E}[X_n] = n(1 - 2p)$ .

Let’s take a moment to think about this result and make sure it seems reasonable. Suppose $p = 0.5$ . This would mean we have an equal chance of moving left or moving right. Over the long run we would expect our final position to be exactly where we started. Plugging in $p = 0.5$ to our equation yields $n(1 - 2 \cdot 0.5) = n(1 - 1) = 0$ . Just as we expected! What if $p = 1$ ? This means we only move to the left. Plugging $p = 1$ into our equation yields $n(1 - 2 \cdot 1) = n(-1) = -n$ . This makes sense! If we can only move to the left then after $n$ steps we would expect to be $n$ steps left of our staring position (the origin as we chose it), the negative direction in our problem setup. We could also choose $p$ to be 0, meaning we only move to the right and we would get $n$ , again just what we would expect!

We can also run a simulation in R to verify our results:

################################################################
# R Simulation
################################################################
# Generate random walk
rand_walk = function (n, p, z) {
  walk = sample(c(-1,1), size=n, replace=TRUE, prob=c(p,1-p))
  for (i in 1:n) {
    z = z + walk[i]
  }
  return(z)
}

n = 1000 # Walk n steps
p = .3 # Probability of moving left
z = 0 # Set initial position to 0
trials = 10000 # Num times to repeate sim
# Run simulation
X = replicate(trials, rand_walk(n,p,z))

# Calculate empirical and theoretical results
empirical = mean(X)
theoretical = n*(1-2*p)
percent_diff = abs((empirical-theoretical)/empirical)*100

# print to console
empirical
theoretical
percent_diff

Printing to the console we see that after 10,000 trials of 1,000 steps each our empirical and theoretical results differ by just 0.046%.

> empirical
[1] 400.1842
> theoretical
[1] 400
> percent_diff
[1] 0.0460288