in Math 330 Words

Distribution Convergence

Let’s do a problem from Chapter 5 of All of Statistics.

Suppose X_1, \dots X_n \sim \text{Uniform(0,1)} . Let Y_n = \bar{X_n}^2 . Find the limiting distribution of Y_n .

Note that we have Y_n = \bar{X_n}\bar{X_n}

Recall from Theorem 5.5(e) that if X_n \rightsquigarrow X and Y_n \rightsquigarrow c  then X_n Y_n \rightsquigarrow cX .

So the question becomes does X_n \rightsquigarrow c  so that we can use this theorem? The answer is yes. Recall that from Theorem 5.4(b) X_n \overset{P}{\longrightarrow} X implies that X_n \rightsquigarrow X . So if we can show that we converge to a constant in probability we know that we converge to the constant in distribution. Let’s show that \bar{X}_n \overset{P}{\longrightarrow} c . That’s easy. The law of large numbers tells us that the sample average converges in probability to the expectation. In other words \bar{X}_n \overset{P}{\longrightarrow} \mathbb{E}[X] . Since we are told that X_i is i.i.d from a Uniform(0,1) we know the expectation is \mathbb{E}[X] = .5 .

Putting it all together we have that:

Y_n = \bar{X_n}^2
Y_n = \bar{X_n}\bar{X_n}
Y_n \rightsquigarrow \mathbb{E}[X]\mathbb{E}[X] (through the argument above)
Y_n \rightsquigarrow (.5)(.5)
Y_n \rightsquigarrow .25

We can also show this by simulation in R, which produces this chart:

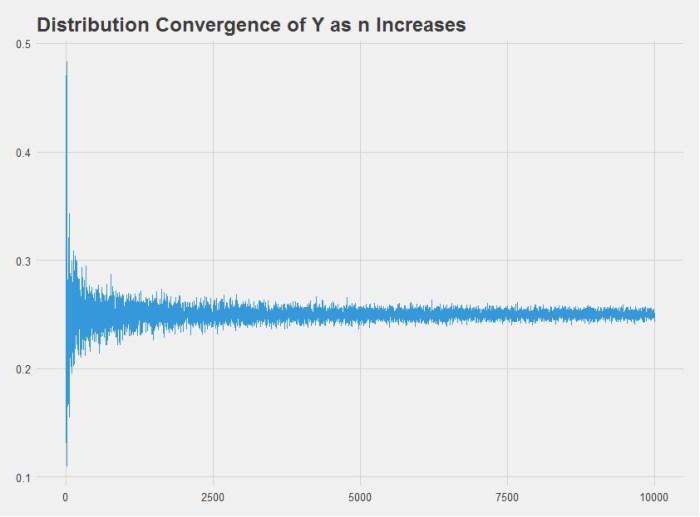
y_convergence

Indeed we also get the answer 0.25. Here is the R code used to produce the chart above:

# Load plotting libraries
library(ggplot2)
library(ggthemes)

# Create Y = g(x_n)
g = function(n) {
  return(mean(runif(n))^2)
}

# Define variables
n = 1:10000
Y = sapply(n, g)

# Plot
set.seed(10)
df = data.frame(n,Y)
ggplot(df, aes(n,Y)) +
  geom_line(color='#3498DB') +
  theme_fivethirtyeight() +
  ggtitle('Distribution Convergence of Y as n Increases')

Leave a comment